In this post, we will cover a couple Vedic math tricks of fast multiplication that are used to mentally multiply fast. We will keep it real, and we will also tell which of the tricks are not so useful and which tricks work the best in exams eventually because you want reliability and speed in the exam. These are the only multiplication tricks you need to be fast in the exam. Please remember not to fret over hundreds of techniques – you will not remember all of them and you will not have reliability. Rather pick the most useful ones and the most reliable ones and practice them more to get the reliability and speed. Let’s start.
Trick 1: Multiplying with 11 or 111 or 1111
Multiplying with 11 is like left shifting the number by one digit and then adding it. 25 times 11 (25 x 11) is nothing but 25 + left shifted 25 = 275
Let’s try 35 x 111 -> add 35 three times by left shifting
Let’s try one more, 63 x 11
Trick 2: Squares of similar numbers ending with 5s
Multiplying two numbers ending in 5s is done by multiplying the left side of the numbers with one of them incremented and then adding 25 at the end. For example, 25 x 25 is (2×3)=6 is the prefix and add 25 as the postfix to it. So, the answer is 625.
Trick 3: Multiplying when the sum of unit digits is 10
This Sutra is called Ekadhikina Purvena. If the sum of the unit digits of the two numbers equals 10, then we can use it.
For example, let’s try the number: 33 x 37. The sum of the unit digits of both numbers (3+7) is 10. So, we can use the sutra here.
(first, digit x one more than the first) (Unit digit of 1st number x Unit digit of the 2nd number) = (3 x 4) (3 x 7) = 1221
Let’s try one more problem: 24 x 26
Again, the unit digits add to 1. So, the LHS is (2 x 3) = 6. And the RHS is (4 x 6) = 24. Answer is 624.
Let’s try one more problem: 163 x 167
This only works when the left side of the numbers are the same. For example, this doesn’t work in the below case.
Trick 4: Multiplication by 9s
Ekanyunena Purvena – When the multiplier is only 9, this sutra may be used to determine the product of two numbers.
Let’s try a problem: 44 x 99=?
The process to solve it is:
Step 1 – Reduce 1 from multiplicand ie. 44-1 = 43
Step 2 – The other part of the answer would be 99 – 43 = 56
Hence the answer is 4356
Alternatively, you can look at it as 44 x 100 – 44 = 4400 – 44 = 4356
Trick 5: Multiplying numbers by 5
Half the number and add 0. Or half the number without the decimal point if there is a decimal point when you half the number
Let’s try one more example: 55 x 5 (when you half 55 you get 27.5, so the answer is 275)
Trick 6: Base Multiplication
Base is a number which has to be a power of 10 and it has to be close to the numbers given to multiply. We then check whether we have to subtract or add the remaining number to achieve that base in each of the individual numbers.
Let’s try another set of numbers:
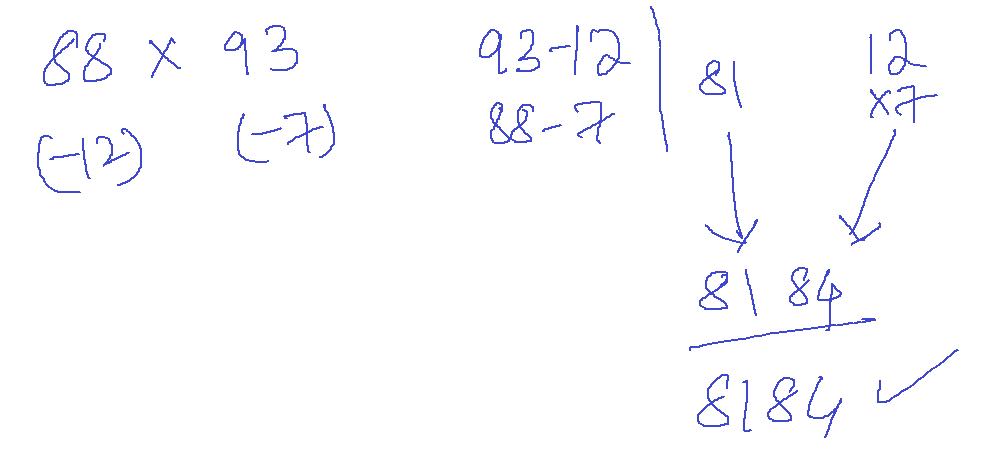
Let’s try another set of numbers:
But again the above problem is not easy because you need to know 16×17 or you need to again to a subset of the above technique for it. So, you see the problem – it is not that easy to apply to numbers away from the base. It is easy to apply to numbers near to the base.
Trick 7: Multiplying mentally with a nearest multiple of 10 in mind
This one is the best in terms of reliability and quickness, but this requires you to become comfortable with multiplying any number with multiples of 10 and 5. Multiplying numbers like 23 x 36 is to multiply with the closest multiple of 10. So, you multiply 36 with 20 first and that is easy 720. And secondly, you multiply 36 x 3 and that is 108. And, add both the results in your mind. 720+108 = 828. Once you get a grip of multiplying with multiples of 10, this can be done really fast.
Let’s try another set of numbers 56 x 88. Multiply 50 with 88 is 4400. Then multiply 6 with 88 which is 48×11 which is 528. Add 528 with 4400 = 4928
Let’s try another set of numbers 34 x 19. Multiply 34 with 20 and minus a 34 out of the result. So, 680 – 34 = 646.
Let’s try another set of numbers 85 x 16:
You need to develop a sense of multiplying with 10, 20, 30, 40, 50, 60, 70, 80, 90 fast, and multiplying with 5 (is nothing half the number and add a zero or remove the decimal – 40×5 = 200)
Let’s try 15 x 85,
Let’s try 15 x 75, 10 x 75 + 5 x75 = 750 + 375 = 1125
This is a very fast approach if you become comfortable with multiplying with multiples of 10 and 5 (is easy).
Trick 8: Multiplying by 9
Say, multiply 64 x 99
Reduce the left number by 1, so 64-1 = 63
Reduce the number 64 from 100 = 36
The answer is 6336
Let’s take one more example – 567 *999
The answer is (567-1)(1000-567) = 566433
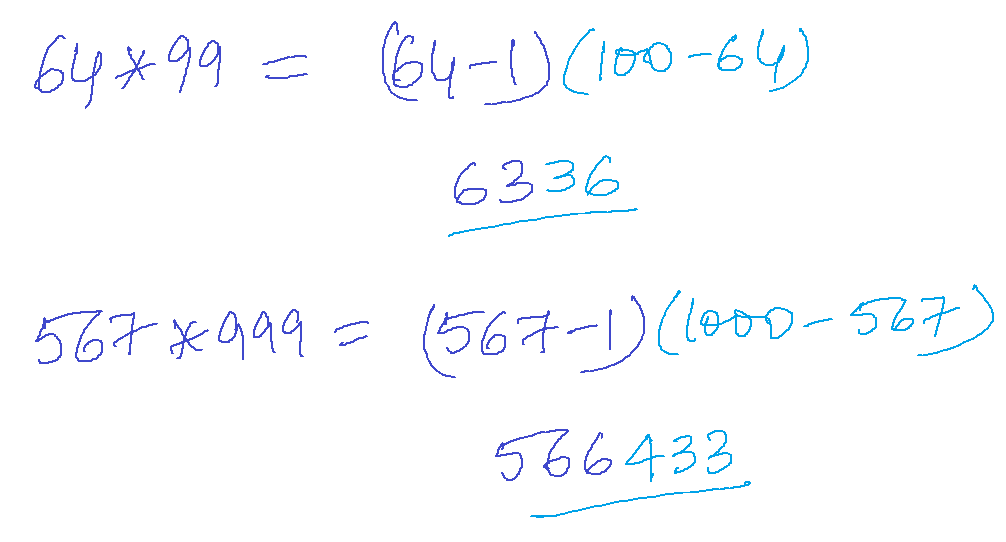
Hope this post is useful to help you in fast multiplications.
Free Vedic Math Quick Multiplication Tricks
Learn more about our online math classes.
You may like to read – the intuition of the math behind integration.




