When you open a tap to fill the bucket, the bucket filled with water is the integration of the tap flow of water over time taken to fill the bucket. Intuitively, integration is addition (integrating – including) and differentiation is division (subtraction or separation).
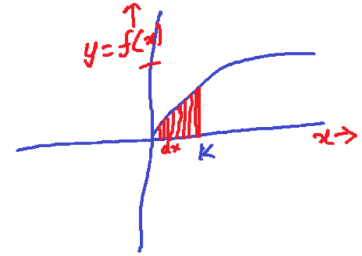
In the above curve, if you want to know the area under the curve (marked red until x value ‘K’), then what you can do is to consider extremely small rectangles with width dx and height y. Multiplying ‘y’ with ‘dx’ will give the area of one of the thin red rectangles. Now, repeat the same and add all of them. But, the y value is different with different heights for each bar. And, that ‘y’ is nothing but f(x).
Therefore, the area under the curve is the sum of many rectangles y*dx, and that sum is integration. So, the area under the curve is integration as below.
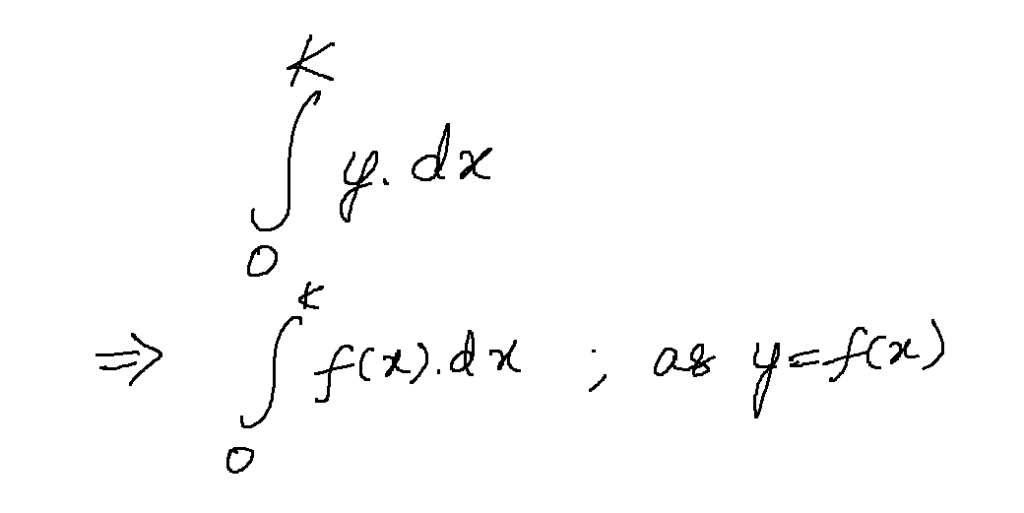
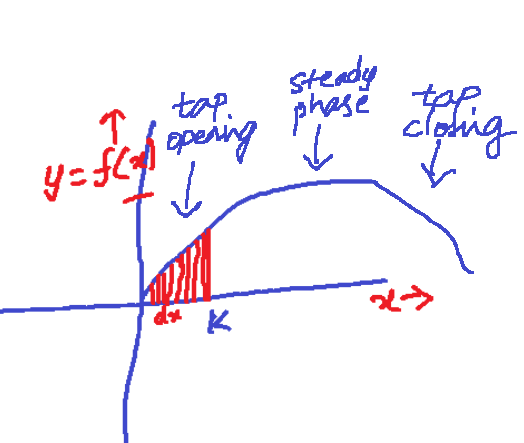
When the tap is opening the rate of flow is going to be varying and a bit slow, and when the tap is closing the rate of flow is again going to be varying and slow. The below function f(x) represents the slower varying rate during the opening and closing phase. The red portion is the amount of water filled in the bucket until time ‘K’ from zero.
Integration is including – it is multiplication and addition. Differentiation is separating – it is division and subtraction.
The rate at which something changes is its derivative, and hence you take the small changes over each of the axes and say ‘dy/dx’. ‘dy’ and ‘dx’ are infinitesimally small changes. This derivative is the slope of the function – and hence it is positive when the function is increasing and negative when the function is decreasing.
For example, if you have to go from one point to another point on a bike, you typically do multiple angle changes of your steering. It is not one major change, but multiple small changes akin to multiple small changes in slope adding up to the major change in direction.


So, to conclude:
Differentiation gives the answer to the question – How rapidly does something change, the slope (the rate of change)?
Integration gives the answer to the question – how do the results of a “variable rate or anything that varies” add up?
Hope this is useful, thank you.
Happy learning at UnicMinds!
You may like to read: Time, Speed, and Distance Practice Problems