Let’s talk about how functions in mathematics is related to coding in this blog.
You must have already written some code in some language and you might’ve used for-loops or while-loops and processed some data using these loops. We typically write different code in various languages to solve some problems like, say sorting an array of numbers, or finding out the largest prime number within a set of numbers, or finding out all the set of possible numbers that add to 10 within an array of numbers.
Typically, we write this code using for-loops and sometimes we may need nested for-loops too to solve some problems. In a nested for loop, essentially we scan the entire array and compare the numbers or do some other computation and repeat that scan for the next selected number again.
So, the amount of work done or complexity of an algorithm like that with nested loops is O(n^2). Because there is one loop that runs from 1 to N and there is another loop nested within the first loop that runs from 1 to N again. For each value in the first loop, the entire second nested loop runs. That is 1x N, when the program runs completely, it becomes NxN = O(n^2).
Computational Complexity of Algorithms
In computer science, you can classify problems based on the complexity of computation into two broad categories. For this, we need to understand a bit of basic mathematics. There are three different types of functions: linear, polynomial, and exponential.
Let’s say f(x) = 3x; this is a linear function.
Let’s say g(x) = 3x^2; this is a polynomial function (x to the power of greater than 1)
Let’s say h(x) = 3^x; this is a exponential function (x is used as a power)
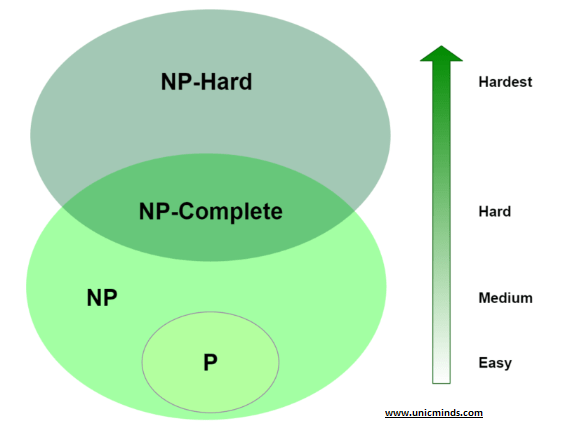
If x has a series of values, which of these functions will result in the highest values? For example, if x value is moving from 1 to 20 which of these functions f(x), g(x) and h(x) will have the highest resulting value? Let’s check the below chart. We have inputted values 1 to 17 in each of these functions and we see that the function h(x) increases the fastest in values and reaches the highest values fairly quickly. Therefore, exponential complexity is the most complex and difficult in terms of computational complexity required and then followed by polynomial complexity.
In computer science, we have a name for problems that have polynomial time complexity in its algortihm and that is called P (complexity) problems. And the problems with exponential time complexity are called NP (complexity) problems. NP problems once solved, whether they’re solved correctly or not -the answer, can be checked in polynomial time but the very solving of it will have an exponential variable in input.
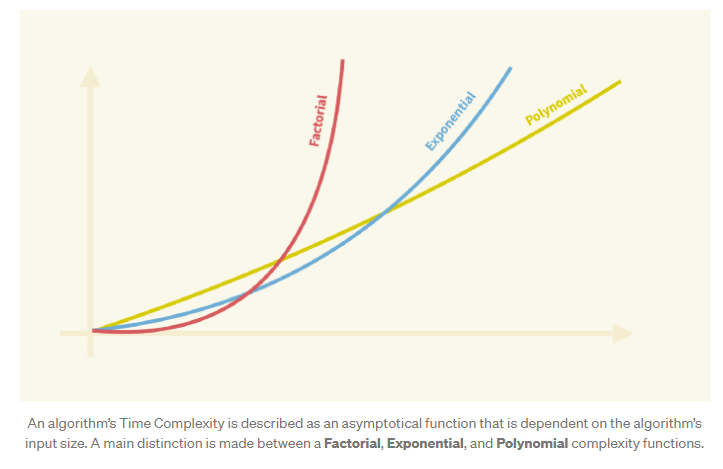
There are many other different class of complexities for various problems. Further NP itself is divided into NP-Hard, NP-Complete and just NP comprising of all. There are other classifications like PSPACE, etc. that we’ll get into later.
But, for now, it is important to understand that your code (essentially algorithms) should take care of space complexity and time complexity. And you should know whether any input or structures are polynomial or exponential in complexity. And we should always try to reduce the complexity for the computer to execute in the fastest manner possible.
NP-Hard problems are the toughest category of problems to solve in polynomial time and there are various prize monies for anyone who can prove a set of stuff around these problems like P=NP and others. So, if you’re interested, write to us at [email protected] and we can teach you the fundamentals of these complexity classes in computer science and build your thinking around it.
Hope this is useful, thank you.